The “Option Pricing using Monte Carlo Simulation” combines both theory and practice and uses model building and option pricing exercises as learning tools to tie in a number of essential topics such as:

the difference between and the significance of the risk-adjusted probabilities of the Black Scholes option pricing model,
the intuition behind the Black Scholes European call option formula,
a preliminary overview of how to create a Monte Carlo simulation model of the Black Scholes solution in Excel,
Estimating errors of and improving results generated from the Monte Carlo simulation model
Pricing vanilla and exotic options using the Monte Carlo simulation model

The course splits the time evenly across 135 minutes between building a model step by step in EXCEL and working with the model to price and value derivative products.

Course Prerequisites

Familiarity with derivative products and comfortable with basic mathematics, numbers and EXCEL.

Course Audience

The course is targeted at intermediate and advance users and is aimed at professionals who deal with pricing, valuation and risk issues related to structured fixed income and foreign exchange transactions.

Course Guide

Here is the structure of the course.

Title	Duration

Session 1 – Black Scholes, N(d1) and N(d2), Monte Carlo Simulator – Theory and Model Review	37:16 mins

Session 2 – Monte Carlo Simulator – Basic Model Walkthrough	10:39 mins

Session 3 – Understanding N(d1) and N(d2) and Option Exercise using Monte Carlo	15:45 mins

Session 4 – Building a Monte Carlo simulator – Foundations	28:37 mins

Session 5 – Using data tables to store Monte Carlo simulation results	11:52 mins

Session 6 – Estimating errors and improving results accuracy	18:46 mins

Session 7 – Pricing Exotic Option using Monte Carlo	18:43 mins

Session One – Black Scholes, N(d1) and N(d2), Monte Carlo Simulator – Theory and Model Review
The risk training course for understanding risk adjusted probabilities of the Black Scholes equation, N(d1) and N(d2), begins with a power point presentation of the theory setting the foundation for appreciating the difference between N(d1) and N(d2). We start with the Black Scholes European call option formula and move on to primary elements of the underlying process behind the generator function for stock prices, drift and diffusion. We address the concept of risk neutrality and conduct various thought experiments around drift and diffusion to understand their impacts on the plot of stock prices over time. We present three interpretations of the intuition behind the Black Scholes European call option formula and then given a preliminary overview of how to create a Monte Carlo simulation model of the Black Scholes solution in Excel.		View a sample of session one
Session Two: Monte Carlo Simulator – Basic Model Walkthrough
In this part we move from our the theory presented in the power point presentation earlier to the practical application of the understanding the difference between N(d1) and N(d2). We given an overview of the Monte Carlo Simulation model built discussing the input cells including the price path generated, the results from the simulation model and the Black Scholes formula, and the results warehouse where results of 30 simulated runs of the model are stored. A brief review of how the simulator can be used to generate and store results and how results could be updated by running multiple iterations.		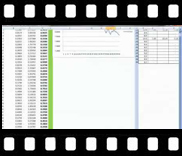View a sample of session two
Session Three: Understanding N(d1) and N(d2) and Option Exercise using Monte Carlo
After having presented the theory behind the process and a general overview of the various elements of the Monte Carlo simulation model together with the procedure for running the model and updating results in our previous finance videos, we now give a thorough walkthrough of the EXCEL sheet of our Monte Carlo simulation model. We begin with how the results of the payment of exercise price and contingent receipt of stock components of the closed form Black Scholes European call option formula are calculated in the model. 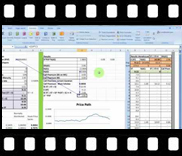Each calculation cell is described in detail, stating precedent and dependent cells, to help with an understanding of: How the model is built, Difference between N(d1) & N(d2), Calculation of the call option value by using Black Scholes formula within the Monte Carlo simulation approach		View a sample of session three
Session Four: Building a Monte Carlo simulator – Foundations
After reviewing the model in earlier session we finally start building the Monte Carlo simulation model for simulating the price path of an equity security and use that path to estimate the value of a call option, a put option and the probability N(d2) of the event ST > X. The session starts with a blank sheet and ends with 10 step simulator that can be used for pricing European call and put options. Building a foundation for Monte Carlo model building with Vanilla options that is later extend to more exotic options. 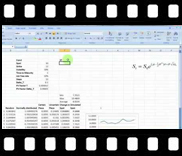This video includes the procedure for generating: A randomly generated path of stock prices Average, minimum, maximum and terminal values for the stock price European call and put option payoffs and their respective premiums		View a sample of session four
Session Five: Using data tables to store Monte Carlo simulation results
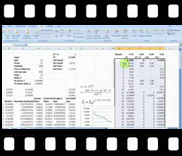
We start by storing results of MC iterations using EXCEL’s “Data Table” function. We then use the stored results to determine the probability of exercise, and values of the call and put options.We use data tables to store results from our option pricing Monte Carlo Simulator and review the sequence of steps required to extend the simulator to support multiple iterations.		View a sample of session five
Session Six: Estimating errors and improving results accuracy
We look at the accuracy of results by comparing our Monte Carlo simulation model option prices with theoretical prices generated by the closed form Black Scholes formula. We introduce the concept of forecasting errors and the impact of increasing iterations on the accuracy and convergence of simulation results.		View a sample of session six
Session Seven: Pricing Exotic Options using Monte Carlo
Now that we have a working Monte Carlo simulation model we extend it to price a number of exotic contracts such as Asian options, barrier options, binary options and lookback options. We take a quick look at the relationship between Vanilla Calls and Knock In and Knock Outs calls, Asset or nothing options and cash or nothing options Look back calls The approach used here can be further extended to price contingent premium options, balloon exercise, participating forwards and other exotic contracts. Pricing for these contracts will be covered in later courses.		View a sample of session seven

Back to top